Uncertainty Quantification for Density Functional Theory Calculations
- Manuel Aldegunde Rodriguez and Nicholas Zabaras
- Mar 17, 2017
- 3 min read
How certain are we of the accuracy of DFT simulations? In this project we try to provide an answer through a framework to quantify the uncertainty in DFT XC functional.


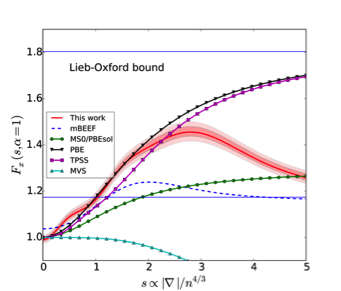
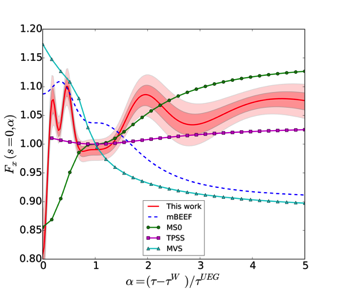
Figure 1 (Top) Magnitude of the coefficients obtained using a RVM for the determination of the hyperparameters. The parameters which go to zero have been plotted with a smaller symbol to highlight the sparsity of the model.(Bottom) Enhancement factor as a function of the reduced density gradient (left) and kinetic energy density (right). The shaded regions for our functional represent one and two standard deviations around the average model.
Results
Using this functional we were able to make predictions with uncertainty bounds for cohesive energies (Fig. 2) and also to propagate this error to other derived quantities such as lattice constants (Fig. 3) and bulk modulus (Fig. 4). Furthermore, using our functional as the basis for G0W0 calculations of the band gap, we were also able to predict the values with a confidence interval (Fig. 5). In terms of molecular energies, we compared the error of our mean functional to others reported in the literature and found that in the molecular sets used for the comparison, our model outperformed even hybrid functional including partially exact exchange contributions.

Figure 2 Box-plot of the equilibrium lattice constants of the elements in the SL20 test set consisting of crystalline solids.

Figure 3 Box-plot of the equilibrium bulk modulus of the elements in the SL20 test set consisting of crystalline solids.

Figure 4 Histograms of the band gap of Si using DFT (grey) and the G0W0 approximation (red) with our XC functional. Gaussian fits are also shown as a guide to the eye. The black vertical line corresponds to the experimental value, the red vertical line to the G0W0 band gap with the average XC functional and the grey vertical line the KS band gap with the average XC functional.
Potential Impact and Innovation
Ab initio material simulations with DFT are used extensively in material design with a given choice of XC functional and assumed to be “exact”. While this has led to some remarkable results, overconfidence in the predictions can result in misjudging the optimal structure for a given application. That is why predictions with uncertainty quantification are an important asset for design. Including this uncertainty in the design process is not trivial and a topic of active research, but being able to incorporate the uncertainty of our material simulations into the design process will definitely advance the field in a considerable way. Instead of proposing a material as the best or even choose a few of the best to reflect our lack of confidence in the results, it will be possible to obtain a set of materials with certain probability of satisfying the desired properties accounting for limited data to train our model and the limited accuracy of the predictions.
Despite the promising results, the work done in this project is only a first step toward the quantification of uncertainty in DFT simulations. For example, the correlation energy was not included in the model. Another area that could be addressed is imposing known constraints in the exchange energy trough different priors in the coefficients, even though this will mean that the model will not be analytically tractable. Finally, another area of interest is the description of the XC energy using different basis functions or nonparametric models such as Gaussian Processes.
Sponsors
This work was funded by the University of Notre Dame and the Computer Science and Mathematics Division of ORNL under the DARPA EQUiPS program is acknowledged.
References
M. Aldegunde, J. R. Kermode and N. Zabaras. Development of an exchange–correlation functional with uncertainty quantification capabilities for density functional theory. Journal of Computational Physics, 311, 173–195 (2016).
U. von Barth. Basic Density-Functional Theory an Overview. Physica Scripta, T109 (T109), 9 (2004).
V. Petzold, T. Bligaard, K.W. Jacobsen, Construction of new electronic density functionals with error estimation through fitting. Topics in Catalysis 55 (5–6), 402-417 (2012).
I.-H. Lee, Y. J. Oh, S. Kim, J. Lee and K.J. Chang, Ab initio materials design using conformational space annealing and its application to searching for direct band gap silicon crystals. Computer Physics Communications 203, 110-121 (2016).








Comments